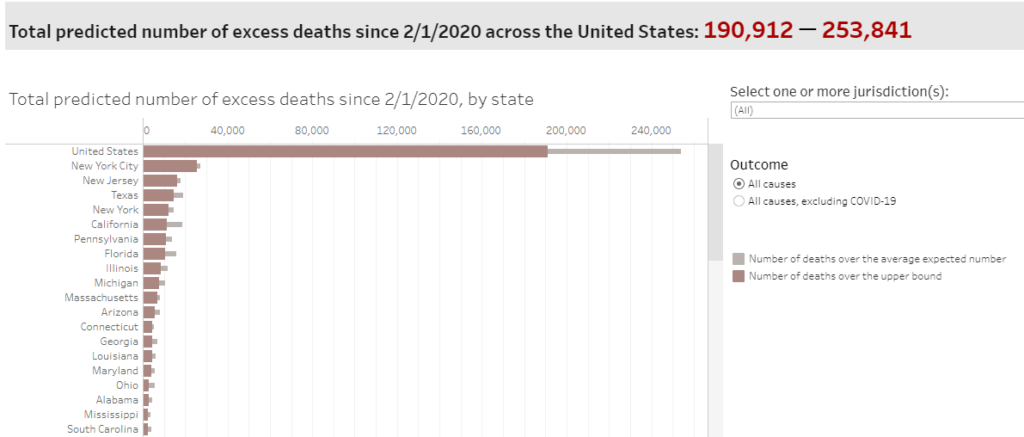
So, are you tired of arguing about things like whether or not the CDC stated that only 6% of the official deaths were due to COVID-19? Me too. (By the way, the easiest way to show that, if anything, the death count is an underestimate is to point out that the excess deaths in the U.S. this year are at about 250,000. Why would that be, if not for COVID-19?)
Well, you’re in luck, because this article is not going to talk about the pandemic (anymore). Let’s all take a break from the daily death toll and the decline of democracy and talk about POKER.
Well, not just about poker, but also about how to approach historical data and carefully draw conclusions from it. There’s no surefire way to answer questions without controlled and randomized experiments, but that doesn’t mean that observational data is worthless. The goal when digging into historical data is to not fool yourself. You need to determine which patterns are meaningful and which are spurious. If there’s a confounding variable that you didn’t think of, you could end up with pie in your face when you present your conclusions to someone who did think of it. Since nobody can think of everything, it’s good practice to consider what answers would make sense, given your understanding of the subject at hand, before you look at the data for answers. Let’s see if I can dodge the pitfalls of data-mining as I look for insights into what makes a successful poker player.
Before we shuffle up and deal, I suggest you brush up on how to play No Limit Texas Hold ‘Em. It’s a fantastic game and it will basically train you how to make good decisions by literally making you pay for superstition and irrationality. You learn that good decision-making doesn’t always result in good outcomes in the short-term, but it will eventually pave the way to success. If you play long enough, you will see that players around you whose strategy depends on their emotional state end up sliding their chips your way, sooner or later. Poker initially appears to be a game of chance, but if you take it seriously, you’ll be rewarded with the realization that you’re no longer a slot-machine player, relying on luck for your success; you’ve become the casino. What may have started out as gambling has become an investment opportunity with a positive expected return.
Anyways, let’s get to the data. A little bird provided me with hand history for over 930,000 online poker hands (at tables limited to 6 players) from about a decade ago. The blinds were $25/$50, which is high enough to be considered “serious” poker. It’s not unusual for a player to have over $10,000 at the table and, in the 3 months of data, three players made a profit of over $100,000 (one player lost over $100,000, so over this time period, poker was a more expensive hobby than golf!).
The first (and most time-consuming) step in a data scientist’s workflow is to get the data into a useable format. In this case, the data came as a semi-structured text file such as the following (names anonymized to match their position at the table)…
Game #5811672164: Table Rock Port (6 max) – $25/$50 – No Limit Hold’em –
Seat 1: MiddlePositionPlayer ($575)
Seat 2: CutoffPlayer ($6,244.75)
Seat 3: ButtonPlayer ($7,694)
Seat 4: SmallBlindPlayer ($6,297)
Seat 5: BigBlindPlayer ($9,522)
Seat 6: UnderTheGunPlayer ($6,100)
SmallBlindPlayer posts the small blind of $25
BigBlindPlayer posts the big blind of $50
The button is in seat #3
*** HOLE CARDS ***
UnderTheGunPlayer folds
MiddlePositionPlayer has 15 seconds left to act
MiddlePositionPlayer folds
CutoffPlayer calls $50
ButtonPlayer folds
SmallBlindPlayer raises to $250
BigBlindPlayer folds
CutoffPlayer calls $200
*** FLOP *** [4h 7s 7c]
SmallBlindPlayer bets $400
CutoffPlayer calls $400
*** TURN *** [4h 7s 7c] [3s]
SmallBlindPlayer checks
CutoffPlayer checks
*** RIVER *** [4h 7s 7c 3s] [Ts]
SmallBlindPlayer checks
CutoffPlayer checks
*** SHOW DOWN ***
SmallBlindPlayer shows [6d 8d] a pair of Sevens
CutoffPlayer shows [Jh Jd] two pair, Jacks and Sevens
CutoffPlayer wins the pot ($1,347) with two pair, Jacks and Sevens
*** SUMMARY ***
Total pot $1,350 | Rake $3
Board: [4h 7s 7c 3s Ts]
Seat 1: MiddlePositionPlayer didn’t bet (folded)
Seat 2: CutoffPlayer showed [Jh Jd] and won ($1,347) with two pair, Jacks and Sevens
Seat 3: ButtonPlayer (button) didn’t bet (folded)
Seat 4: SmallBlindPlayer (small blind) showed [6d 8d] and lost with a pair of Sevens
Seat 5: BigBlindPlayer (big blind) folded before the Flop
Seat 6: UnderTheGunPlayer didn’t bet (folded)
Since I wanted data summarized by player, I created a custom computer program with class objects in code that represented players and tracked of all of their stats, such as “looseness” (VPIP, or Voluntarily Put In Pot, which is the percentage of hands a player plays) and “aggression” (the ratio of bets/raises to checks/calls). Each player “object” also had properties tracking their profit, number of hands played, etc. Note that the profit for each player is not simply the total size of the pots they won. For the example above, the CutoffPlayer won a $1347 pot, but $650 was his own money, so the profit for the hand was $697. The need to extract implicit information of interest is why custom code is necessary for the import and that there is no simple “just load it into a database” approach.
After the file was imported, the summary statistics for each player were exported to a text file for easy analysis in Excel. I also tracked stats for 6 additional virtual “players” representing each of the 6 seats at the table: Small Blind, Big Blind, Under the Gun, Middle Position, Cutoff, and Dealer Button. These stats duplicated the actual player stats, but allowed me to look at how the average player acted depending on their position for the hand.
If you’re not familiar with them, these are the positions at a 6-max table…

Another good reason to track stats by position is so that we could do a “reality check” and ensure that the imported data makes sense. For example, players generally play fewer hands when in early position, because the more players that follow you in the betting order, the bigger your disadvantage. We would expect to find that players in unfavorable positions at the table would not only be tighter (more selective about the hands they play) but also more passive (playing more defensively by betting and raising less, in order to limit the size of their losses).
Let’s see what the data says.
| Position | Looseness (VPIP) |
| Button | 36% |
| Cutoff | 22% |
| Middle Position | 22% |
| Under the Gun (UTG) | 20% |
| Big Blind (BB) | 22% |
| Small Blind (SB) | 28% |
So, players who were first to act (UTG) only played 20% of their hands. For a sense of what this means in terms of poker hands, if you were to rank the two-card hand types according to how well they match up against random cards, the top 20% would include every hand at least as good as the following: Ace-Three suited (>=A3s), Ace-Seven offsuit (>=A7), King-eight suited (K8s, K9s, KTs, KJs, KQs), King-Ten offsuit (KT, KJ, KQ), Queen-Ten suited (QTs, QJs), Queen-Jack, or pairs of fives or higher (>=55). (Note: “suited” just means that the two hole cards have the same suit.)
As expected, the Looseness increases as the player sits closer and closer to the Button (the Dealer position). Sitting in the best position allowed players to play over a third of the time. It’s trickier to know what to expect in terms of looseness of the blinds, since the Small Blind is in a horrible position, but has already paid some of the price of playing. Similarly, the Big Blind only needs to add money to the pot if somebody raises before the flop. Nevertheless, these stats look reasonable, so I’m feeling pretty good about the imported and organized data.
How about Aggression (ratio of bets/raises to checks/calls)? Again, you would expect players in good positions to be betting and raising more (playing offense), while players in bad positions are checking and calling more (playing defense) to keep the pot size under control. Let’s see if the data matches this expectation.
| Position | Aggression |
| Button | 2.1 |
| Cutoff | 1.9 |
| Middle Position | 1.9 |
| Under the Gun (UTG) | 1.8 |
| Small Blind (SB) | 0.9 |
| Big Blind (BB) | 0.4 |
Aggression almost perfectly sorts the positions from best to worst! The only exception is that the small blind is the worst seat after the flop (first to act), but these players were more aggressive than the big blind. This can be explained by the fact that the small blind at least chose to enter the hand (at a discount), whereas the big blind sometimes saw the flop with two random cards (if nobody raised before the flop, they can “check” and continue in the hand for free). So again, the data looks reasonable given what we know about poker strategy.
While there aren’t any notable surprises in the data yet, if you believe in the wisdom of the masses, it does confirm that you should play looser (more hands) when you have a good position at the table, playing about a third of all hands dealt when you have the dealer button. It also backs up the idea that players in the blinds should be primarily checking and calling, while players in good position should be betting and raising. The better your position, the more aggressive you can be; with the dealer button you can bet/raise more than twice as often as you check/call.
Now comes the part that really matters: profit. Which positions are the most profitable and which ones cost you chips?
| Position | Success (profit per hand) |
| Button | $11.09 |
| Cutoff | $6.85 |
| Under the Gun (UTG) | $6.68 |
| Middle Position | $6.19 |
| Small Blind (SB) | $(9.48) |
| Big Blind (BB) | $(15.50) |
This clearly shows the importance of position. All things being equal, the player sitting with the dealer button is expected to make almost twice as much money as anyone else! It’s hard to see image how one seat can be so much more profitable than the seat next to it, but there is one thing that’s unique when you have the button: if everyone folds to you pre-flop, it’s just you against the blinds (and they have to act first in every future round of betting). It’s a great spot to raise and win immediately or build a pot where you have the advantage of acting last. Even the cutoff seat right before the dealer runs the risk of the dealer calling or raising their bet and having to play the rest of the hand out of position. In short, the dealer is the only one who’s guaranteed to have a positional advantage.
It’s not a surprise that the blinds are the most expensive seats at the table, since you are literally forced to bet, regardless of your cards. The profitability of the other positions sorts them as expected, except for one: players under the gun (first to act after the blinds) made more money per hand than players in the middle position. Since there’s no good reason why this should be generally true, I wouldn’t read too much into it. The difference is only $0.50 per hand at the $50 big blind table stakes so it may be that there were just a few monster hands that swayed the results.
Note that we don’t just look at total dollars won, since sometimes there are fewer than 6 players at the table and the seats in the worst positions are empty. Technically, the players at the middle position made more profit than the players under the gun ($793k vs. $544k), but since there were 128k hands dealt with a player in the middle position and only 81k hands dealt with a full table (and therefore included a player sitting under the gun), the UTG position made more profit per hand.
It’s good to see that the small blinds and big blinds are losing less than $25 and $50 per hand respectively, or they would have been able to improve their results by simply folding their hands every time they were in the blinds! I was a bit surprised to see that every position other than the blinds was actually profitable on average. Since we know that the poker site is making money from the rake, the total losses must exceed the total wins (in this case $153,500 went from the players to the online cardroom during the months observed). Surprisingly, the losses for the two blinds ($4.75M) more than offset the total winnings from the other four positions at the table ($4.60M).
Let’s move on from stats by position and look at the stats by player. The big question is whether or not playing tight and aggressive (TAG) is generally the winning formula for poker. Excel has a nice Data Analysis add-in that allows you to easily run multiple linear regressions. Basically, you just highlight the profit per hand column as the target variable and select the looseness and aggression columns as your predictive variables and see what it comes up with…
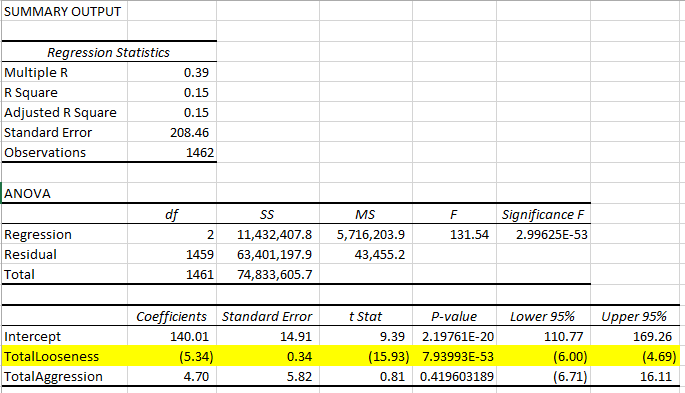
While the general conclusions seem reasonable, there’s something a bit strange about the p-value; it’s off the charts! Are there any gotchas we should be looking for? Remember what we’re predicting here: the profit per hand. Well, what if someone just played one hand and won or lost a lot?
Sure enough, there was one player, who sat down with $5,000, ended up going all-in on his first hand and losing, never to play again. His profit per hand is -$5000 and he played 100% of his hands. Similarly, there are 15 others who all played exactly one hand and lost more than $1000, never to return. These outliers need to be removed from consideration, because the extreme looseness and results dwarf any of the values you’d see with regular players and will warp our conclusions. Let’s limit the data to players with at least 10 hands played and see how that changes things…
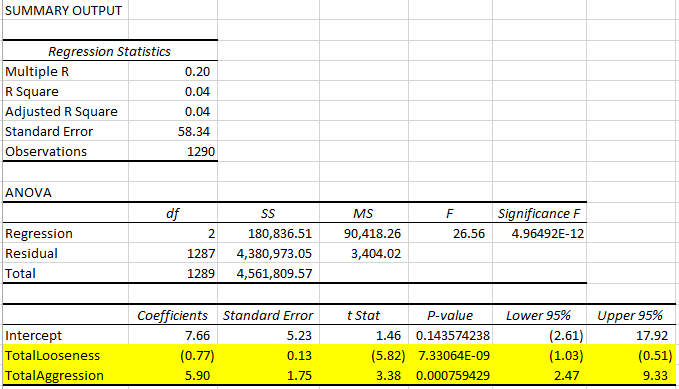
Well, the p-value is still pretty outrageous, but we peeked at the raw data and nothing jumped out as an obvious problem, so we’ll run with it. Looking at these results, I’d state with confidence that the tighter players generally make more money. Obviously, you can’t take this to the extreme and say that the best player would play 0% of the hands, but you can say that when comparing any two players in this data set of 1290 players, the tighter player is probably the more profitable one. And the tighter the player, the more profitable you’d expect him or her to be.
What about aggression? Now that we’ve removed the outliers, it appears that more aggressive players are also significantly more profitable on average.
The R-squared value of 0.04 is very low, which tells you that knowing only aggression and looseness can only “explain” 4% of the variation in the profitability between the players. More specifically, if you used the equation suggested by the coefficients above [profit per hand = $7.66 – 0.77 * Looseness + 5.90 * Aggression], your predicted profit would only have a 0.2 correlation with the actual player profitability in the data (R-squared is the correlation squared – a 1.0 correlation would be a perfect prediction, and a 0.0 correlation would mean your prediction may as well have been completely random).
Recall that while we have extremely high confidence that profitability is associated with aggression and negatively associated with looseness, we still have to take this with a grain of salt since we’re just analyzing historical data and not the results of a controlled experiment. There could be a hidden confounding variable that we should be considering. For example, what if we break down the data by how many players are at the table? Conventional wisdom states that as the number of players at the table decreases, you should loosen up the range of hands you play and also play more aggressively. Let’s see what we get if we re-run our regression analysis on 6-player, 5-player, 4-player, 3-player, and heads-up situations.
| Number of Players | Looseness Coefficient | p-value | Aggression Coefficient | p-value |
| 6 | $(1.28) | 0.000 | $1.76 | 0.281 |
| 5 | $(0.47) | 0.007 | $3.16 | 0.110 |
| 4 | $0.02 | 0.934 | $1.34 | 0.499 |
| 3 | $0.15 | 0.607 | $0.58 | 0.822 |
| 2 | $(0.12) | 0.680 | $9.61 | 0.004 |
There are a couple interesting things here! The first is that the cost of playing loosely is only significant when there are 5 or 6 players at the table. Another finding: playing aggressively isn’t particularly predictive of success (although generally good) unless it’s one-on-one. These results are a bit surprising, but not necessarily out of left field (which is a good thing when you’re worried about data-mining). In summary, you want to be the tightest player at the table when it’s 5 or 6 handed. But if it’s heads-up, you want to be the aggressive player.
Let’s look at how the average players actually played, depending on their number of opponents. And, more interestingly, let’s see how the 10 biggest winners (by total profit) and the 10 biggest losers played…
| # | Avg Looseness | Avg Aggression | Top 10 Loose. | Top 10 Aggress. | Bot 10 Loose. | Bot 10 Aggress. |
| 6 | 28.7% | 1.12 | 22.7% | 1.97 | 29.3% | 1.20 |
| 5 | 29.8% | 1.02 | 24.3% | 1.92 | 28.3% | 1.37 |
| 4 | 34.2% | 1.05 | 29.8% | 1.89 | 28.9% | 1.14 |
| 3 | 40.8% | 1.09 | 33.8% | 1.59 | 37.5% | 1.49 |
| 2 | 50.3% | 0.97 | 47.5% | 1.57 | 45.9% | 1.35 |
As expected, everyone loosens up as the number of opponents decreases. However, notice that the 10 biggest winners are consistently playing 4-7% fewer hands than the average player (with the exception of heads-up situations). Interestingly, both the best and the worst players are more aggressive than average, but the best players do consistently bet and raise more than they check and call. Again, there may be other variables at play, such as that the best players are more likely to seek positional advantage (which in turn leads to more aggressive play). However, describing them as Tight and Aggressive does appear appropriate.
Next time, we’ll discuss more specifically how the most profitable players play. The great thing about poker hand history files is that you can often see cards at showdown and then match them up with the betting patterns from the player earlier in the hand for analysis. With enough data, you’ll have a pretty complete sense of the types of hands people play and how they play them. To me, this is what makes poker so interesting. It needs to be studied in the context of what people actually do, rather than what is best in some theoretical sense. It’s not the optimal strategy you seek; it’s the exploitive one.