Okay, so now that the president has shown us that COVID-19 is a piece of cake as long as you have a tiger blood transfusion at the ready, we can focus on more important things: I’m honored to say that poker legend Daniel Negreanu glanced at my last blog entry and … said that it didn’t add up.
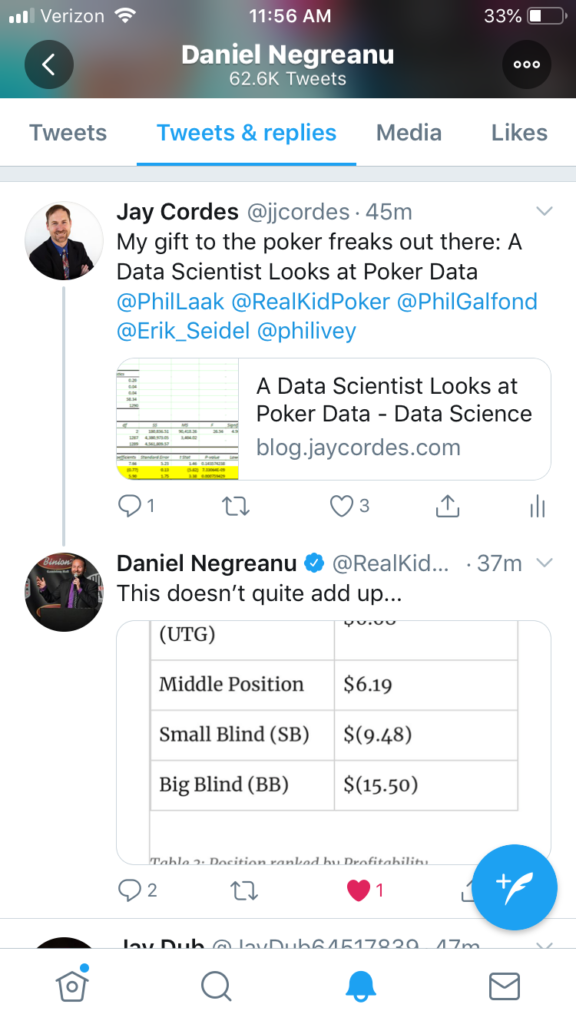
I displayed the total stats by position, summarizing the data to just show the aggregates without any filtering or funny stuff. Nothing to explain, right? It’s the total profitability for each of the positions at the 6-max tables.
The problem is, as my friend pointed out, “shouldn’t you use only the data for full tables? Apples and oranges, otherwise.” What do you think? Here’s my original table, which is the total profit for each position divided by the total hands played from each position…
| Position | Success (profit per hand) |
| Button | $11.09 |
| Cutoff | $6.85 |
| Under the Gun (UTG) | $6.68 |
| Middle Position | $6.19 |
| Small Blind (SB) | $(9.48) |
| Big Blind (BB) | $(15.50) |
If you’re assuming that each position was played the same number of times, there’s a big problem: the numbers add up to an average profit greater than zero! Poker sites don’t run for free, and they certainly don’t give away more money than they take in. The numbers aren’t wrong, but an assumption is; every hand dealt has a big blind, but not every hand played has an Under the Gun player (there are often seats empty at the table). Allow me to present a new version of the table with profit by position only when the table is full:
| Position | Success (profit per hand) |
| Button | $10.92 |
| Cutoff | $7.53 |
| Under the Gun (UTG) | $6.54 |
| Middle Position | $5.17 |
| Small Blind (SB) | $(11.03) |
| Big Blind (BB) | $(20.21) |
Even though this table is based on less data, it lines up better with expectations. If you add up the numbers now, you get -$1.07, which is the average rake (it ranges from $0 to $3). The ranking of the seats by profitability is still the same, even with that odd quirk of UTG being more profitable than the middle position, despite being a worse position. However, you’ll notice that the increase in profitability is smoother. The dealer position is no longer so unusually profitable (the dealer’s relative advantage evidently grows as the number of opponents decreases) while all of the other non-blind positions are about the same. The takeaway lesson is this: make sure you’re showing people what they’re expecting; don’t just show aggregate numbers for the entire dataset as a matter of principle.
Anyway, recall that last time, we found that, overall, the top 10 players (by total profit) were tighter and more aggressive than the bottom 10 players. Let’s look more closely at how the top 10 vs. the bottom 10 played when the tables were full. The top players pocketed a total of $508,000 ($8.35 per hand), while the bottom players lost $338,000 (-$10.84 per hand).
Another thing you’d expect to see from good players is a better ability to manage “tilt”, which is when people’s emotions get out of control and they’re unable to continue playing their “A game” after a big loss. Since we’re looking at data for $50 big blind tables, let’s call a big loss one that exceeds $1000. This happened less than 1% of the time for the biggest winners, so it’s pretty rare.
According to a paper co-authored by my professor buddy Gary Smith, “…experienced poker players typically change their style of play after winning or losing a big pot—most notably, playing less cautiously after a big loss, evidently hoping for lucky cards that will erase their loss.”
As a group, the biggest winners played 20.7% of their hands in the following round (6 hands dealt) after a big loss, while the biggest losers played 35.3%! That’s a dramatic difference, especially when you consider that the looseness in general (not preceded by big wins or losses) for these groups was 21.1% and 28.1%, so the top players displayed no tilt at all, while the bottom players went a bit crazy. After a big loss, the loss per hand for the bottom players more than doubled ($-9.43 to $-23.20 per hand).
| Normal Loose % | Normal Profit | Loose % after big loss | Profit after big loss | Loose % after big win | Profit after big win | |
| Top 10 | 21.1% | $8.59 | 20.7% | $6.93 | 19.8% | $5.79 |
| Bottom 10 | 28.1% | ($9.43) | 35.3% | ($23.20) | 32.7% | ($11.59) |
So, what about hand ranges? We know that top players are more selective, but what specifically does that mean? As I started looking through sample hands for the top players, I noticed that an unusual number of them were making aggressive plays because they were short-stacked (had less than $1000 when the blinds are $25/$50). There were a lot of hands where someone would raise before the action got to them and they would just respond with an all-in, especially if the raise came from the button…
| Game: | No Limit |
| Blind: | $25/ $50 |
| Hand History converter courtesy of pokerhandreplays.com | |
| Seat1: | Player 1 | ($5,172) | Big Blind |
| Seat2: | Player 2 | ($5,250) | |
| Seat3: | Player 3 | ($7,630) | |
| Seat4: | Player 4 | ($5,222) | |
| Seat5: | Player 5 | ($16,680) | Dealer |
| Seat6: | Player 6 | ($1,000) | Small Blind |
| Dealt to Player 6 | |
  |
| Player 2 | FOLD |
| Player 3 | FOLD |
| Player 4 | FOLD |
| Player 5 | RAISE | $175 |
| Player 6 | ALL-IN | $975 |
| Player 1 | FOLD |
| Player 5 | CALL | $825 |












| Player 6 SHOWS |
  |
| Player 5 SHOWS |
  |
| Player 6 | wins the pot: $2,050 |
(Note: the all-in raise was to $1000, but $25 was already in the pot from the SB)
Then I realized there were a LOT of hands like this and that they were primarily from two of the ten players. Sure, enough, when I looked more closely, it turned out that they were buying in as short-stacks, doubling up, and then switching tables, only to buy-in as short-stacks again – a strategy described as “hit and run” or “rat-holing”, which can be a surprisingly profitable and annoying strategy in cash-games.
Because people think of short-stacks as being in a position of weakness in tournaments, many don’t realize that it’s actually a strategic advantage in cash games (well, the pros do, which is why they’re generally not fans of rat-holers). Not only is it relatively simple to play (often, it’s just one all-in re-raise before the flop), it puts the bigger stacks in very awkward positions. Sometimes, they’re basically forced mathematically to call a bet, even if they suspect they have the worst of it.
Consider the hand above, but suppose the short-stack player (QJs) showed his hand as he went all-in, so the original raiser (44) could make a perfectly informed decision. The decision that 44 faced was whether or not to call another $825 for a chance at $2050. Since $825 / $2050 is 40.24%, a Hold’em Calculator tells us that it’s a clear call (44 vs. QJs has a 48% chance of winning). By making the correct call here, the original raiser can expect to win 48% * $2050 = $984 (hence, “pos EV” or positive expected value for the call). That’s a good amount better than the $825 it cost to call the bet, but it’s worse than if the player had just sat out the hand and never had to shell out $1000 for the experience. And this was in the case where the short-stack player had a mediocre hand! Often, an all-in from the blinds here means a medium or high pair, in which case the raiser would win less than 20% of the time. So, the call is not automatic by any means! In summary, when an initial raiser gets shoved on by a short-stack, they’re put in a very tough spot in which they’re just trying to lose as little of their money as possible.
From an earlier life, I know a bit about this short-stack style of play (shhh!) so I wasn’t completely surprised to see two short-stackers in the list of the top 10 most profitable players. They weren’t as profitable per hand as the others top players, but they made up for it with volume (often being a short-stack is so easy to play, you can play many tables simultaneously). Most notably, the short-stackers were MUCH more aggressive than the other players, due to the large number of all-ins and relatively few check/call type hands…
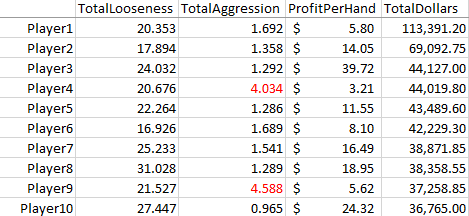
Since these players truly had a distinctive style, I lumped them together; let’s call them a prototypical successful short-stacker. Here’s what I found:
Under the Gun: When seated in the worst position, they showed down the following hands (recall that “AKs” means Ace-King suited, while “KJo” means King-Jack offsuit):
[A A][Q Q][T T][9 9][5 5][AKs][AQs][ATo][KJo]
Assuming that they chose their playable hand range according to how well they rank against a random hand in a showdown, this looks like about the top 14% of possible hands (55 is the worst hand in the group by this metric, winning only 60.32% vs. a random hand, so their range would include each hand type down to “55” at the link above). This is significantly tighter than the typical player UTG (20%), so if you see an experienced short-stack player raising from UTG, you’ve been warned about what you’re up against!
[Note: if you want to figure out the top x% range yourself, just put your list of ranked hand types in Excel with a column next to them showing the number of ways to get dealt each type of hand. Card combinatorics tell us that pairs can happen 6 ways, suited cards 4 ways, and unsuited non-pairs can be dealt 12 ways. If you include all possible hand types in your list, the “ways” column should add up to 1326, the total number of different two-card poker hands. Now, you can calculate the total “ways” for the set of hands you’re interested in, divide it by 1326, and you’ve got your percentage!]
Middle Position: In this position, they showed down a wider range:
[A A][Q Q][J J][8 8][T T][7 7][AKs][AJs][A7s][A6s][AKo][AQo][AJo][ATo][A9o][KJo][QJo]
This looks like the top 20% hands (every hand above QJo here). Hmm, 5 players left in the hand, 1 in 5 = 20%? It’s possible these players didn’t base their playable hand ranges on historical data, but rather just on the number of opponents left to act (in which case they may actually play 1/6 = 16.7% of their hands from UTG).
A typical hand (player 4 is the short-stacker)…
| Game: | No Limit |
| Blind: | $25/ $50 |
| Hand History converter courtesy of pokerhandreplays.com | |
| Seat1: | Player 1 | ($1,366) | Small Blind |
| Seat2: | Player 2 | ($6,643) | Big Blind |
| Seat3: | Player 3 | ($5,729) | |
| Seat4: | Player 4 | ($1,297) | |
| Seat5: | Player 5 | ($1,159) | |
| Seat6: | Player 6 | ($14,769) | Dealer |
| Dealt to Player 4 | |
  |
| Player 3 | FOLD |
| Player 4 | RAISE | $100 |
| Player 5 | FOLD |
| Player 6 | CALL | $100 |
| Player 1 | FOLD |
| Player 2 | RAISE | $400 |
| Player 4 | ALL-IN | $1,197 |
| Player 6 | FOLD |
| Player 2 | CALL | $897 |












| Player 4 SHOWS |
  |
| Player 2 SHOWS |
  |
| Player 4 | wins the pot: $2,769 |
You can see why the aggression rating for these guys is off the charts. When dealt a pair and playing with a short-stack, it doesn’t make sense to call a raise and hope to hit a set, because the pot size won’t be big enough to justify the gamble. In this case, the short-stacker correctly predicted that the hand would be a coin flip, so he bet $800 for an even chance at $2800.
Cutoff Position: They showed a similar range here, so it looks like top 20% again…
[A A][K K][Q Q][T T][9 9][5 5][3 3][AKs][AQs][AKo][AQo][KJo][KTo][AJo][ATo][KQs][KTs]
The only hand outside of the top 20% here is 33, which only wins 53.69% vs. a random hand. It’s just hard to fold pairs!
Dealer Position: Here’s where their ranges really opened up. It looks to me like they could be raising with any above-average hand…
[A A][Q Q][T T][7 7][4 4][3 3][AKs][AQs][AJs][A7s][A6s][AKo][AQo][AJo][ATo][A9o][A7o][K5s][KQo][J7s][98o]
The loosest hands here are 98 offsuit (48.1% vs. random hand!) and J7 suited (52.32% vs. random hand).
Blinds: The sample hand at the beginning of this article shows that they will re-raise all-in out of the blinds even with a hand like QJ suited, which barely makes the top 20%, so it appears that they’re expecting other players to be just as loose as they are with their button raises. Here’s the whole set of hands they re-raised out of the blinds with…
[A A][K K][Q Q][J J][T T][9 9][8 8][7 7][6 6][5 5][4 4][2 2][AKs][AQs][AJs][ATs][A9s][A7s][A6s][AKo][AQo][AJo][ATo][A9o][A8o][A6o][A5o][K7s][KQo][KJo][KTo][QJs][T7s][T9s][98s]
In summary, they’re playing tighter than normal in the early position, looser than normal from the button, and much more aggressive than other profitable players. If they’re not in the blinds and someone raises before them, they typically push all-in with the top 10% of dealt hands. This is consistent with their overall strategy: find spots where (based on very limited information) they think they have an above average hand against their opponent’s range and then shove all of their chips in and hope for the best. It’s a pretty simple approach, and worked well ($80k profit in a few months for the two of them at the $25/$50 tables isn’t bad!)
If you’re new to poker, I’d recommend buying in with a short-stack and playing selectively and aggressively like these guys. The deeper the stacks, the more complicated the game gets and the more vulnerable you are against the more experienced opponents. If you don’t have many chips and Daniel Negreanu raises pre-flop and you push all-in on him, it doesn’t matter that he’s ten times better than you. He has to decide whether to call or fold and can’t bluff you out. Be warned however: he might have read this article and you may not be happy when he flips over his cards!